




 |
 |
 |
 |
 |
 |
 return to the Idea Bank index |
(Share your ideas, too!)
|
| Spring Math Ideas from Math Cats News, issue #5 (April 26, 2001) by Wendy Petti During this invigorating time of year, I like to spend as much time outdoors as possible, and I hope you do, too. But we can always keep an eye out for opportunities to enjoy math even while we are enjoying a beautiful spring day. Here are some ideas: 1) Outdoor estimation activities * Look at a tree and try to estimate its circumference and its diameter, and then figure out how to measure it. * Guess how many blades of grass might be encircled by a large rubberband dropped casually on a playing field or a yard, and then get down on your hands and knees and start counting! * Lie on your back and watch a cloud moving past, and try to predict how long it will take to finish passing a treetop... then start a stopwatch! * Measure your shadow at different times of day. * Try to locate the largest and smallest blooms on a flowering bush or in a garden bed, estimate their dimensions, and then measure them and compare. 2) Charting changes in the air Children as young as Kindergarten can learn to enter data in spreadsheets (and/or record daily numbers in a list, if a spreadsheet program is not available). You can help the children in your life to set up a spreadsheet to record data and display it with a simple graph which will automatically reflect changes when you update the data. What sorts of data? Here are just a few ideas from an endless supply of possibilities:
* daily temperature highs and lows
But we do also need to keep in mind the wise words from the "Inchworm" song [from the musical, Hans Christian Andersen]: |
| More Spring Math Ideas Dear Wendy, Having just read your newsletter with some ideas for outdoor activities I thought I could mention some that are taking place in my school. Although the class is in Year 8 I'm sure some of the activities could be adapted. Design a playground to fit inside a given space at your school - using mathematical shapes and working out their areas.
Calculate the height of trees
Yours, [NOTE from Math Cats: Here is a link to a school page on making and using your own clinometer. It will open in a new window. If you follow their link to "GLOBE" for details, you need to scroll about halfway down a very long page to find the diagram and instructions for making the clinometer. http://www.northstar.k12.ak.us/schools/upk/lter/aswegrow/clinometer.html If those instructions seem too complex, you can get a rough measurement of the height of a tree by measuring its shadow and measuring the shadow of a 12" ruler rising straight up at a 90 degree angle from the ground. Divide the length of the tree's shadow by the length of the ruler's shadow. If, for example, the tree's shadow is 20 times longer than the ruler's shadow, then the tree would be around 20 feet tall. Or, if you compare the ruler's actual length to its shadow's length, then you can assume that the tree's height compared to its shadow will be the same ratio. These estimates may be inaccurate if the shadow measurements are taken near the middle of the day when the sun is overhead, and/or if the tree's crown is very broad and dense.]
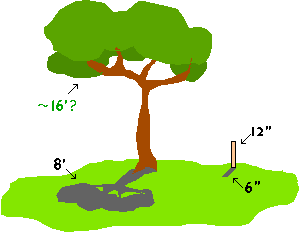 (In this simple example, the ruler is twice as long as its shadow, so we estimate that the tree is twice as tall as its shadow, which would make it around 16 feet tall.)  top top |
|
|
| © copyright 2000 - Wendy Petti of Math Cats. All Rights Reserved. |